Question

an airplane takes 5 hours with 35 mi/h tail wind. the return took 7 hours against the same wind. find the speed of the plain in no winds

Answer 1

Answer: 210 mph

Explanation:

Let X be the speed of the plane in calm air.

With a tailwind, the plane travels at X + 35 mph.

Against the wind, the plane travels at X - 35 mph.

We know that the plane travels the same distance on both trips. Let this distance be D.

We can set up two equations based on the given information:

Equation 1: D = (X + 35) * 5

Equation 2: D = (X - 35) * 7

Since the distance is the same in both equations, we can equate them:

(X + 35) * 5 = (X - 35) * 7

5X + 175 = 7X - 245

-2X = -420

X = 210 mph

Therefore, the speed of the plane in calm air is 210 mph.

Answer 2

210 miles/hour

Explanation:

Let's denote the speed of the airplane in still air as
`\sf s` (in miles per hour).

When the airplane is flying with a tailwind, its effective speed is increased by the speed of the wind. So, with a tailwind of 35 mph, the effective speed is
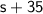`\sf s + 35` mph.

When the airplane is flying against the wind, its effective speed is decreased by the speed of the wind. So, against the same wind, the effective speed is
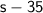`\sf s - 35` mph.

The formula for speed is distance divided by time:

`\sf \textsf{Speed} = \frac{\textsf{Distance}}{\textsf{Time}}`

Let
`\sf d` be the one-way distance.

For the first leg (with the wind), the time is 5 hours:

`\sf s + 35 = (d)/(5)`

For the return leg (against the wind), the time is 7 hours:

`\sf s - 35 = (d)/(7)`

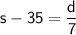
Now, we have a system of two equations with two unknowns:

`\sf \begin{cases} s + 35 = (d)/(5) \\ s - 35 = (d)/(7) \end{cases}`

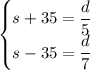
Let's solve this system to find
`\sf s`, the speed of the airplane in still air.

First, let's isolate
`\sf d` in both equations:

`\sf d = 5(s + 35)`

`\sf d = 7(s - 35)`

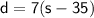
Now, set these two expressions equal to each other since they represent the same distance:

`\sf 5(s + 35) = 7(s - 35)`

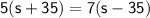
Now, solve for
`\sf s`:

`\sf 5s + 175 = 7s - 245`

`\sf 2s = 420`

`\sf s = 210`

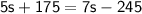
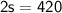
So, the speed of the airplane in still air is
`\sf 210` miles per hour.