Question

Do it get the points

Answer 1

`\boxed{\sf (-8, 25)\;(-3, 15)} \longleftrightarrow \boxed{\sf (-17, -1)\;(-97, -41)}`

`\boxed{\sf (36, -46)\;(14, 4)} \longleftrightarrow \boxed{\sf (-5, 36) \;(20, 47)}`

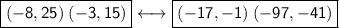
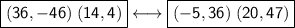
Explanation:

The slope of a line perpendicular to the original line is the negative reciprocal of the original slope. Therefore, to calculate the perpendicular slope between two points, find the slope of the original line that passes through these points using the slope formula, then take its negative reciprocal.

`\boxed{\begin{array}{l}\underline{\textsf{Slope formula}}\\\\\large\text{$m=(y_2-y_1)/(x_2-x_1)$}\\\\\textsf{where:}\\\phantom{w}\bullet\;\;m\; \textsf{is the slope.}\\\phantom{w}\bullet\;\;(x_1,y_1)\;\textsf{and}\;(x_2,y_2)\;\textsf{are two points on the line.}\\\\\end{array}}`

`\hrulefill`

Points (-8, 25) and (-3, 15)

`\textsf{Slope $(m)$}=(15-25)/(-3-(-8))=(-10)/(5)=-2`

`\textsf{Perpendicular Slope $\left(-(1)/(m)\right)$}=-(1)/(-2)=(1)/(2)`

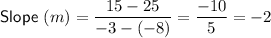
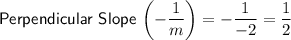
Points (-17, -1) and (-97, -41)

`\textsf{Slope $(m)$}=(-41-(-1))/(-97-(-17))=(-40)/(-80)=(1)/(2)`

`\textsf{Perpendicular Slope $\left(-(1)/(m)\right)$}=-(1)/((1)/(2))=-2`

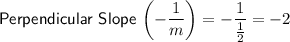
Therefore, the slope of the line that passes through points (-8, 25) and (-3, 15) is perpendicular to the slope of the line that passes through points (-17, -1) and (-97, -41), and vice versa.

`\hrulefill`

Points (36, -46) and (14, 4)

`\textsf{Slope $(m)$}=(4-(-46))/(14-36)=(50)/(-22)=-(25)/(11)`

`\textsf{Perpendicular Slope $\left(-(1)/(m)\right)$}=(11)/(25)`

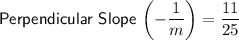
Points (-5, 36) and (20, 47)

`\textsf{Slope $(m)$}=(47-36)/(20-(-5))=(11)/(25)`

`\textsf{Perpendicular Slope $\left(-(1)/(m)\right)$}=-(1)/((11)/(25))=-(25)/(11)`

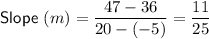
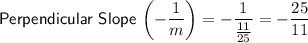
Therefore, the slope of the line that passes through points (36, -46) and (14, 4) is perpendicular to the slope of the line that passes through points (-5, 36) and (20, 47), and vice versa.