Question

PRECALC QUESTION!!!!

Answer 1

(a) (1, 0) and (-6, 0)

(b) (0, -2)

(c) x = -1 and x = -3

(d) Horizontal asymptote: y = 1
No slant asymptotes.

(e) See attachment.

Explanation:

Given rational function:

`R(x)=(x^2+5x-6)/(x^2+4x+3)`

Factor the numerator and the denominator of the given rational function:

`\begin{aligned}\textsf{Numerator:}\quad x^2+5x-6&=x^2+6x-x-6\\&=x(x+6)-1(x+6)\\&=(x-1)(x+6)\end{aligned}`

`\begin{aligned}\textsf{Denominator:}\quad x^2+4x+3&=x^2+3x+x+3\\&=x(x+3)+1(x+3)\\&=(x+1)(x+3)\end{aligned}`

Therefore, we can write function R(x) as:

`R(x)=((x-1)(x+6))/((x+1)(x+3))`

`\hrulefill`

x-intercepts

The x-intercepts are the points at which the graph of the function intercepts the x-axis, so the values of x when y = 0.

To find the x-intercepts of R(x), set the function to zero and solve for x:

`((x-1)(x+6))/((x+1)(x+3))=0`

`(x-1)(x+6)=0`

`x-1=0\implies x=1`

`x+6=0\implies x=-6`

Therefore, the x-intercepts are at (1, 0) and (-6, 0).

`\hrulefill`

y-intercept

The y-intercept is the point at which the graph of the function intercepts the y-axis, so the value of y when x = 0.

To find the y-intercept of R(x), substitute x = 0 into the function and solve for y:

`R(0)=((0-1)(0+6))/((0+1)(0+3))`

`R(0)=((-1)(6))/((1)(3))`

`R(0)=(-6)/(3)`

`R(0)=-2`

Therefore, the y-intercept is at (0, -2).

`\hrulefill`

Vertical asymptotes

Vertical asymptotes occur at the x-values that make the denominator of a rational function zero. Therefore, to find the vertical asymptotes of R(x), set the denominator to zero and solve for x:

`(x+1)(x+3)=0`

`x+1=0 \implies x=-1`

`x+3=0 \implies x=-3`

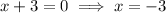
Therefore, the equations of the vertical asymptotes are x = -1 and x = -3.

`\hrulefill`

Horizontal & slant asymptotes

As the degree of the numerator is equal to the degree of the denominator, the horizontal asymptote is the result of dividing the highest degree term of the numerator by the highest degree term of the denominator:

`y=(x^2)/(x^2)=1`

Therefore, the equation of the horizontal asymptote is y = 1.

A slant asymptote occurs when the degree of the numerator polynomial is exactly one greater than the degree of the denominator polynomial. Therefore, there are no slant asymptotes since the degree of the numerator polynomial is the same as the degree of the denominator polynomial.