Question

Calculate the length of AD in the triangle-based pyramid below.

Give your answer to 2 d.p.
(Not drawn accurately)

Answer 1

`AD=70.42\; \sf cm\; (2\;d.p.)`

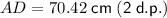
Explanation:

Edge AD of the given triangular-based pyramid is the hypotenuse of right triangle ABD.

To find the length of AD, we first need to determine the length of one of the legs of ΔABD. To do this, we can find the length of BD by applying the tangent trigonometric ratio to right triangle BCD.

`\boxed{\begin{array}{l}\underline{\textsf{Tangent trigonometric ratio}}\\\\\sf \tan(\theta)=(O)/(A)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$\theta$ is the angle.}\\\phantom{ww}\bullet\;\textsf{$O$ is the side opposite the angle.}\\\phantom{ww}\bullet\;\textsf{$A$ is the side adjacent the angle.}\end{array}}`

In triangle BCD:

• θ = ∠D = 33°
• O = BC = 37 cm
• A = BD

Substitute these values into the tangent ratio and solve for BD:

`\tan(33^(\circ))=(37)/(BD)`

`BD=(37)/(\tan(33^(\circ)))`

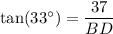
Now, apply the sine trigonometric ratio to right triangle ABD to find the length of AD.

`\boxed{\begin{array}{l}\underline{\textsf{Sine trigonometric ratio}}\\\\\sf \sin(\theta)=(O)/(H)\\\\\textsf{where:}\\\phantom{ww}\bullet\;\textsf{$\theta$ is the angle.}\\\phantom{ww}\bullet\;\textsf{O is the side opposite the angle.}\\\phantom{ww}\bullet\;\textsf{H is the hypotenuse (the side opposite the right angle).}\end{array}}`

In triangle ABD:

• θ = ∠A = 54°
• O = BD = 37 / tan(33°)
• H = AD

Substitute these values into the sine ratio and solve for AD:

`\sin(54^(\circ))=((37)/(\tan(33^(\circ))))/(AD)`

`AD=((37)/(\tan(33^(\circ))))/(\sin(54^(\circ)))`

`AD=(37)/(\tan(33^(\circ))\sin(54^(\circ)))`

`AD=70.4249775...`

`AD=70.42\; \sf cm\; (2\;d.p.)`

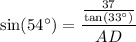
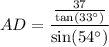
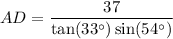
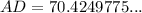
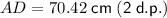
Therefore, the length of edge AD is 70.42 cm, rounded to two decimal places.