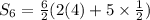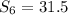Question

The 10th, 4th and 1st term of an A.P are three consecutive find the common ratio of the G.P and the sum of the 6th term, taking the 1st term to be 4

Answer 1

Common ratio=1/2

Sum of first 6 terms of an A.P=31.5

Explanation:

Let a be the first term and d be the common difference of an A.P

a=4

nth term of an A.P

`a_n=a+(n-1)d`

Using the formula

`a_4=a+3d=4+3d`

`a_(10)=a+9d=4+9d`

According to question

We know that

For G.P

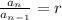`(a_n)/(a_(n-1))=r`=Common ratio

`r=(4+3d)/(4+9d)=(4)/(4+3d)`

`(4+3d)/(4+9d)=(4)/(4+3d)`

`(4+3d)^2=(4)/(4+3d)`

`16+9d^2+24d=16+36d`

`9d^2+24d-36d-16+16=0`

`9d^2-12d=0`

`3d(3d-4)=0`

`d=0, d=4/3`

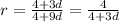
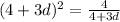
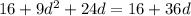
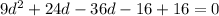
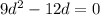
Substitute the value of d

When d=0

`r=(4)/(4+3d)=(4)/(4+0)=1`

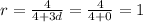
When d=4/3

`r=(4)/(4+3* (4)/(3))=(1)/(2)`

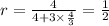
But we reject d=0 because if we take d=0 then the terms are not consecutive terms of G.P

Sum of n terms of an A.P

`S_n=(n)/(2)(2a+(n-1)d)`

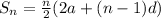
Using the formula

Substitute n=6 and d=1/2

`S_6=(6)/(2)(2(4)+5* (1)/(2))`

`S_6=31.5`