Question

As sand leaks out of a hole in a container, it forms a conical pile whose altitude is always the same as the radius. If the height of the pile is increasing at a rate of 6 inches/minute, find the rate at which the sand is leaking out when the altitude is 10 inches.

Answer 1

The rate at which sand is leaking out when the altitude is 10 inches is 600π cubic inches per minute, calculated using the volume of a cone formula and the given rate of the height's increase.

Step-by-step explanation:

To find the rate at which the sand is leaking out, we need to use the formula for the volume of a cone, which is V = (1/3)π
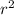`r^2`h, where V is the volume, r is the radius, and h is the height. Since the altitude is always equal to the radius, we can rewrite this as V = (1/3)π
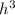`h^3`. We are given that the height of the pile is increasing at a rate of 6 inches/minute, which we can denote as dh/dt = 6. To find the rate of change of the volume, dV/dt, we take the derivative of the volume with respect to time, which gives us dV/dt = π
`h^2` · dh/dt. Plugging in the numbers, dV/dt = π·
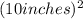`(10 inches)^2`·(6 inches/minute), we find that the sand is leaking out at a rate of π· 100 · 6 cubic inches per minute.

Thus, the rate of sand leakage when the altitude is 10 inches is dV/dt = 600π cubic inches per minute.