Answer: 3sec²(3x)
Explanation:
The definition of derivative is:
f'(x) =
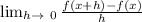
From the given problem, we can see that tan3(x+h) is f(x+h) and tan3x is f(x).
Since we now know what f(x) is, we can find f'(x), or the limit of (tan3(x+h) - tan3x)/h where h is approaching 0.
f(x) = tan3x
f'(x) = sec²(3x) * 3
f'(x) = 3sec²(3x)