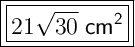Question

Didnt get taught this yet. but its on my homework and the support video isnt helping.

Answer 1

Check the picture below.

`\textit{area of a triangle}\\\\ A=\cfrac{1}{2}bh ~~ \begin{cases} b=base\\ h=height\\[-0.5em] \hrulefill\\ b=7√(10)\\ h=6√(3) \end{cases}\implies A=\cfrac{1}{2}\cdot 7√(10)\cdot 6√(3)\implies A= 7√(10)\cdot 3√(3) \\\\\\ A=(7\cdot 3)√(10\cdot 3)\implies \boxed{A=21√(30)}`

Answer 2

`21\sqrt {30}\; \sf cm^2`

Explanation:

The formula for calculating the area of a triangle is:

`\boxed{\begin{array}{l}\underline{\textsf{Area of a triangle}}\\\\A=(1)/(2)bh\\\\\textsf{where:}\\\phantom{w}\bullet\;\;\textsf{$b$ is the base of the triangle.}\\\phantom{w}\bullet\;\;\textsf{$h$ is the height of the triangle.}\end{array}}`

In the given right triangle:

• 
  `\textsf{Base,}\;b=7√(10)\;\sf cm`

• 
  `\textsf{Height,}\;h=6√(3)\;\sf cm`

Substitute the base and height into the area formula:

`A=(1)/(2) \cdot 7 √(10) \cdot 6 √(3)`

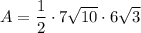
Apply the commutative property of multiplication, which states that when you multiply numbers, you can change the order of them without changing the result.

`A=(1)/(2) \cdot 6\cdot7\cdot √(10) \cdot √(3)`

Multiply the numbers 1/2 and 6:

`A=3\cdot7\cdot √(10) \cdot √(3)`

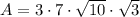
Multiply the numbers 3 and 7:

`A=21\cdot √(10) \cdot √(3)`

`\textsf{Apply the radical rule:} \quad \sqrt{\vphantom{b}a}\cdot √(b)=√(a\cdot b)`

`A=21\cdot \sqrt {10 \cdot 3}`

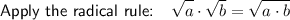
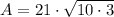
Multiply the numbers 10 and 3:

`A=21\cdot \sqrt {30}`

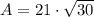
Therefore, the area of the triangle as a surd in its simplest form is:

`\Large\boxed{\boxed{21\sqrt {30}\; \sf cm^2}}`