Answer:
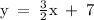
Explanation:
To find the equation of a line parallel to -4y = 32 - 6x, we first need to rewrite this equation in slope-intercept form, y = mx + b, where m is the slope and b is the y-intercept.
-4y = 32 - 6x
Divide both sides by -4:
y = -8 + (3/2)x
So the slope of this line is 3/2. Since we want a line parallel to this one, it will have the same slope of 3/2.
Now we can use the point-slope form of a linear equation to find the equation of the line that passes through (0,7) with a slope of 3/2:
y - y1 = m(x - x1)
where m = 3/2 and (x1,y1) = (0,7)
y - 7 = (3/2)(x - 0)
Simplifying:
y - 7 = (3/2)x
y = (3/2)x + 7
So the equation of the line parallel to -4y = 32 - 6x that passes through the point (0,7) is y = (3/2)x + 7.