The correct order for simplifying the expression
![\(\sqrt[4]{567x^9 \cdot y^(11)}\)](https://img.qammunity.org/2024/formulas/mathematics/college/x6t9wazgn6vwihaz6t3lwsvi44sprs7s8u.png) using the properties of rational exponents is:
using the properties of rational exponents is:
![1. \((567x^9 \cdot y^(11))^(1/4)\). 2. \(3x^2 \cdot y^2 \cdot (7^(1/4) \cdot x^(1/4) \cdot y^(3/4))\). 3. \((81 \cdot 7)^(1/4) \cdot x^(9/4) \cdot y^(11/4)\). 4. \(3x^2 \cdot y^2 \cdot (7x \cdot y^3)^(1/4)\). 5. \(3x^2 \cdot y^2 \cdot \sqrt[4]{7x \cdot y^3}\). 6. \((81)^(1/4) \cdot (7)^(1/4) \cdot x^(2 + 1/4) \cdot y^(2 + 3/4)\). 7. \((3^4)^(1/4) \cdot 7^(1/4) \cdot x^(2 + 1/4) \cdot y^(2 + 3/4)\). 8. \(3^(1-4) \cdot 7^(1/4) \cdot x^2 \cdot x^(1/4) \cdot y^2 \cdot y^(3/4)\)](https://img.qammunity.org/2024/formulas/mathematics/college/n8w8lv9miho8pif7xn2lbnpthz8ymg7qfp.png)
First, we rewrite
![\(\sqrt[4]{567x^9 \cdot y^(11)}\)](https://img.qammunity.org/2024/formulas/mathematics/college/x6t9wazgn6vwihaz6t3lwsvi44sprs7s8u.png) as
as
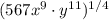 . Then, we apply the rules: simplify the numbers inside the parentheses, distribute the exponent to each term, and combine like terms. This results in expressions with smaller exponents. The correct steps ensure that we handle each part of the expression properly, leading to the simplified form.
. Then, we apply the rules: simplify the numbers inside the parentheses, distribute the exponent to each term, and combine like terms. This results in expressions with smaller exponents. The correct steps ensure that we handle each part of the expression properly, leading to the simplified form.
1.
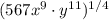
2.
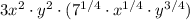
3.
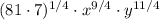
4.
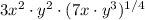
5.
![\(3x^2 \cdot y^2 \cdot \sqrt[4]{7x \cdot y^3}\)](https://img.qammunity.org/2024/formulas/mathematics/college/pvj3zsikv04m98fwyc2kcgsmin45x3vw24.png)
6.
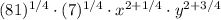
7.
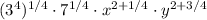
8.
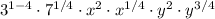
These steps correctly simplify the expression using the properties of rational exponents.