Question

Use Descartes' Rule of Signs to determine the possible numbers of positive and negative real zeros.

Answer 1

Positive: 3,1

Negative: 1

Answer 2

(a) Possible number(s) of positive real zeros: 3

(b) Possible number(s) of negative real zeros: 1

Explanation:

Descartes' Rule of Signs tells us the maximum number of positive and negative roots.

Positive root case

`f(x)=-3x^4+2x^3-x^2+9x+7`

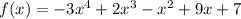
As there are 3 sign changes, the maximum possible number of positive roots is 3.

Negative root case

`\begin{aligned}f(x)&=-3(-x)^4+2(-x)^3-(-x)^2+9(-x)+7\\&=-3x^4-2x^3-x^2-9x+7 \end{aligned}`

As there is one sign change, the maximum possible number of negative roots is 1.