Question

in a positive number of two digits, the sum of the digits is 15, if the digits are interchanged, the number is increased by 9. Find the number.​

Answer 1

the number is 78

Explanation:

call x is the tens digit (0<x<9)

y is the unit digit (0
`\leq`y
`\leq`9)

we have:

10y+x=
`\oveline{yx}` (1)

10x+y=
`\overline{xy}` (2)

acording (1),(2) and the topic we have: (10y+x)-(10x+y)=9 ⇔9y-9x=9

⇔y-x=1 (3)

and x+y=15 (4)

from (3), (4) we have a system of equation

`\left \{ {{y-x=1} \atop {x+y=15}} \right.`

⇔
`\left \{ {2y=16} \atop {x+y=15}} \right.`

⇔
`\left \{ {{y=8} \atop {x+8=15}} \right.`

⇔
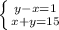
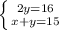
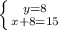
`\left \{ {{y=8} \atop {x=7}} \right.` (conditions are satified)

the number is 78