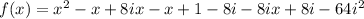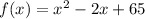Question

NO LINKS!!

A polynomial f(x) with real coefficients and leading coefficient 1 has the given zeros and degree. Express f(x) as a product of linear and/or quadratic polynomials with real coefficients that are irreducible over R(real numbers).

1. 7 + 6i, -4 + i; degree 4

f(x) = _____________

2. 4, -6 - 2i; degree 3
f(x) = __________

3. 1 + 8i; degree 2

f(x) = ______________

Answer 1

`\textsf{1.} \quad f(x)=(x^2-14x+85)(x^2+8x+17)`

`\textsf{2.} \quad f(x)=(x-4)(x^2+12x+40)`

`\textsf{3.} \quad f(x)=x^2-2x+65`

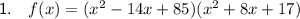
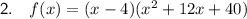
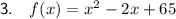
Explanation:

Question 1

Given information:

• Polynomial function with real coefficients.
• Zeros: 7 + 6i, -4 + i
• Leading coefficient: 1
• Degree: 4

For any complex number
`z=a+bi`, the complex conjugate of the number is defined as
`z^*=a-bi`.

If f(z) is a polynomial with real coefficients, and z₁ is a root of f(z)=0, then its complex conjugate z₁* is also a root of f(z)=0.

Therefore, if f(x) is a polynomial with real coefficients, and (7 + 6i) is a root of f(x)=0, then its complex conjugate (7 - 6i) is also a root of f(x)=0.

Similarly, if (-4 + i) is a root of f(x)=0, then its complex conjugate (-4 - i) is also a root of f(x)=0.

Therefore, the polynomial in factored form is:

`f(x)=1(x-(7 + 6i))(x-(7 - 6i))(x-(-4 + i))(x-(-4 - i))`

`f(x)=(x-7-6i)(x-7+6i)(x+4-i)(x+4+i)`

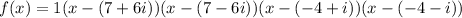
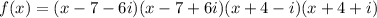
Expand the polynomial:

`f(x)=(x-7-6i)(x-7+6i)(x+4-i)(x+4+i)`

`f(x)=(x^2-14x+49-36i^2)(x^2+8x+16-i^2)`

`f(x)=(x^2-14x+49-36(-1))(x^2+8x+16-(-1))`

`f(x)=(x^2-14x+85)(x^2+8x+17)`

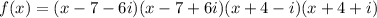
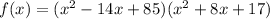
Question 2

Given information:

• Polynomial function with real coefficients.
• Zeros: 4, -6 - 2i
• Leading coefficient: 1
• Degree: 3

For any complex number
`z=a+bi`, the complex conjugate of the number is defined as
`z^*=a-bi`.

If f(z) is a polynomial with real coefficients, and z₁ is a root of f(z)=0, then its complex conjugate z₁* is also a root of f(z)=0.

Therefore, if f(x) is a polynomial with real coefficients, and (-6 - 2i) is a root of f(x)=0, then its complex conjugate (-6 + 2i) is also a root of f(x)=0.

Therefore, the polynomial in factored form is:

`f(x)=1(x-4)(x-(-6-2i))(x-(-6+2i))`

`f(x)=(x-4)(x+6+2i)(x+6-2i)`

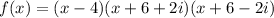
Expand the polynomial:

`f(x)=(x-4)(x^2+6x-2ix+6x+36-12i+2ix+12i-4i^2)`

`f(x)=(x-4)(x^2+12x+36-4i^2)`

`f(x)=(x-4)(x^2+12x+36-4(-1))`

`f(x)=(x-4)(x^2+12x+40)`

Question 3

Given information:

• Polynomial function with real coefficients.
• Zeros: 1 + 8i
• Leading coefficient: 1
• Degree: 2

For any complex number
`z=a+bi`, the complex conjugate of the number is defined as
`z^*=a-bi`.

If f(z) is a polynomial with real coefficients, and z₁ is a root of f(z)=0, then its complex conjugate z₁* is also a root of f(z)=0.

Therefore, if f(x) is a polynomial with real coefficients, and (1 + 8i) is a root of f(x)=0, then its complex conjugate (1 - 8i) is also a root of f(x)=0.

Therefore, the polynomial in factored form is:

`f(x)=1(x-(1+8i))(x-(1-8i))`

`f(x)=(x-1-8i)(x-1+8i)`

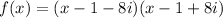
Expand the polynomial:

`f(x)=x^2-x+8ix-x+1-8i-8ix+8i-64i^2`

`f(x)=x^2-2x+1-64(-1)`

`f(x)=x^2-2x+65`