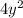Question

AREA The area of the rectangle in the figure is 32xy square units. Find the width of the rectangle. Write any variables in alphabetical order.

8xy

Answer 1

`4y^(2)`

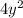
Explanation:

A = Area

w = width

l = length

`A=lw`

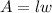
in this equation the area is
`32xy^(3)` and the length is
`8xy`.

To find the equation we simply have to divide the area (
`32xy^(3)`) by the length (
`8xy`).

`32xy^(3) =(8xy)w`

When dividing, it's important to remember two things:

1. A variable divided by itself is one
2. To divide a variable by the same variable with a lower exponent we have to subtract

Using these two rules, we divide the common bases (number by number, x by x, y by y):

`(32)/(8)=4`

`(x)/(x)=1`

`(y^(3) )/(y)=y^(2)`

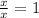
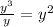
Multiplying all of them together, we find that the width is:

`4y^(2)`