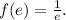Question

Let f be the function defined by f(x)=lnxx. what is the absolute maximum value of f

Answer 1

The function
`\( f(x) = (ln(x))/(x) \)` attains its absolute maximum value at ( x = e ), and the maximum value is
`\( (1)/(e) \)`.

Step-by-step explanation:

The critical points of the function
`\( f(x) = (ln(x))/(x) \)`occur where its derivative is zero or undefined. Taking the derivative using the quotient rule, we get:

`\[ f'(x) = (1 - ln(x))/(x^2) \]`

Setting the numerator equal to zero gives
`\( ln(x) = 1 \),` and solving for ( x ) gives ( x = e ). Now, to determine whether this critical point is a maximum, minimum, or neither, we can use the second derivative test. The second derivative is:

`\[ f''(x) = (ln(x) - 3)/(x^3) \]`

Substituting ( x = e ) into the second derivative, we find that
`\( f''(e) = (1 - 3)/(e^3) = -(2)/(e^3) \)`. Since the second derivative is negative at ( x = e ), the function has a local maximum at this point.

To find the absolute maximum, we also need to consider the behavior of ( f(x) ) as ( x ) approaches zero and infinity. As ( x ) approaches zero, ( f(x) ) approaches negative infinity, and as \( x \) approaches infinity, ( f(x) ) approaches zero. Therefore, the absolute maximum value occurs at ( x = e ), and the maximum value is
`\( f(e) = (1)/(e) \).`

Answer 2

The absolute maximum value of the function does not exist.

Step-by-step explanation:

The function is f(x) = ln(x/x). To find the absolute maximum value of the function, we can analyze its graph. Since the natural logarithm function is always decreasing, the graph of f(x) will also be a declining curve.

When x = 0, f(x) = ln(0/0), which is undefined. However, as x approaches 0 from the right, the function approaches negative infinity. Therefore, there is no absolute maximum value for f(x).