Question

There ae 46 legs in a zoo exihibit. every animal has either 2 or 4 legs. the expression 2m+4n is the total number of legs for m 2 legged animals and n 4 legged animals in the exihibit

a. list possible values for m and n so that the total number of legs is 46


b. The number of 2 legged animas is 2 more than the number of 4 legged animals. how many of each are in the exhibit?


c. The number of legs in the exhibit increases by 4. what might account for this increase?

Answer 1

Explanation:

a. Possible values for m and n to achieve a total number of 46 legs are: m = 23 and n = 11; m = 22 and n = 12; m = 21 and n = 13; m = 20 and n = 14; m = 19 and n = 15; m = 18 and n = 16.

b. If the number of 2 legged animals is 2 more than the number of 4 legged animals, there must be 24 2 legged animals and 22 4 legged animals in the exhibit (24 + 22 = 46).

c. The increase in the number of legs in the exhibit might be due to the addition of a new animal to the exhibit. If the new animal has 4 legs, the total number of legs in the exhibit will increase by 4.

Answer 2

a) Possible values of m and n:

• m = 23, n = 0
• m = 21, n = 1
• m = 19, n = 2
• m = 17, n = 3
• m = 15, n = 4
• m = 13, n = 5
• m = 11, n = 6
• m = 9, n = 7
• m = 7, n = 8
• m = 5, n = 9
• m = 3, n = 10
• m = 1, n = 11

b) 9 two-legged animals and 7 four-legged animals.

c) Either 1 four-legged animal or 2 two-legged animals have been added to the exhibit.

Explanation:

Given expression:

2m + 4n = 46

where:

• m = 2 legged animals
• n = 4 legged animals

Part a

Calculate the greatest number of four-legged animals by dividing the total number of animals by 4:

`\implies 46 / 4 = 11.5`

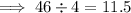
Therefore, the greatest number of four-legged animals is 11.

When there are no four-legged animals, n = 0.

Substitute n = 0 into the given equation:

`\begin{aligned}\implies 2m+4(0)&=46\\2m&=46\\ m&=23\end{aligned}`

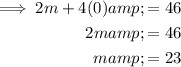
Therefore, there are 23 two-legged animals when there are no four-legged animals.

Each time the number of four-legged animals increases by 1, the number of two-legged animals decreases by 2.

Therefore, the possible values for m and n so that the total number of legs is 46 are:

• m = 23, n = 0
• m = 21, n = 1
• m = 19, n = 2
• m = 17, n = 3
• m = 15, n = 4
• m = 13, n = 5
• m = 11, n = 6
• m = 9, n = 7
• m = 7, n = 8
• m = 5, n = 9
• m = 3, n = 10
• m = 1, n = 11

Part b

If the number of two-legged animals is 2 more than the number of four-legged animals then:

• m = 9, n = 7

Therefore, there are 9 two-legged animals and 7 four-legged animals.

Part c

If the number of legs in the exhibit increases by 4, then either:

• 1 four-legged animal has been added to the exhibit, or
• 2 two-legged animals have been added to the exhibit.