Answer:
2145
Explanation:
Here is the formula for the sum of the first n terms.
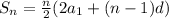
Here is the formula for the nth term.

We are given
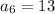
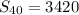
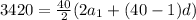
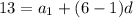
We don't have a lot to work with but we can get it done.
Lets solve for
 in
in
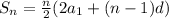 .
.
Multiply each term by
 .
.
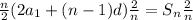
Simplify.
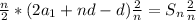
Apply the distributive property.
/(n) =S_n(2)/(n)](https://img.qammunity.org/2024/formulas/mathematics/high-school/h0ld195v2cdlyqx6iu5izcfkphg0n39cbt.png)
Simplify.


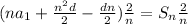
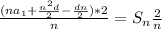
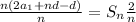
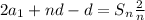
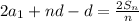
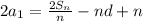
Divide each term by 2.
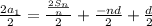
Simplify.
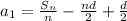
Insert our answer for
 into
into

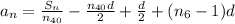
I continued my work on paper. I will attach it below.