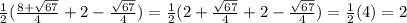Question

A soccer ball is kicked from 3 feet above the ground. the height,h, in feet of the ball after t seconds is given by the function h=-16t^2+64t+3

find the time it takes for the ball to return back to ground level.

find the maximum height rescued by the ball.

Answer 1

Here's our equation.


`h=-16t+64t+3`

We want to find out when it returns to ground level (h = 0)

To find this out, we can plug in 0 and solve for t.


`0 = -16t+64t+3 \\ 16t-64t-3=0 \\ use\ the\ quadratic\ formula\ (-b\±√(b^2-4ac))/(2a) \\ (-(-64)\±√((-64)^2-4(16)(-3)))/(2*16) = (64\±√(4096+192))/(32)`


`= (64\±√(4288))/(32) = (64\±8√(67))/(32) = (8\±√(67))/(4) = \boxed{(8+√(67))/(4)\ or\ 2-(√(67))/(4)}`

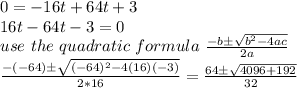
So the ball will return to the ground at the positive value of
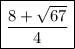
`\boxed{(8+√(67))/(4)}` seconds.

What about the vertex? Simple! Since all parabolas are symmetrical, we can just take the average between our two answers from above to find t at the vertex and then plug it in to find h!


`\frac{1}2((8+√(67))/(4)+2-(√(67))/(4)) = \frac{1}2(2+(√(67))/(4)+2-(√(67))/(4)) = \frac{1}2(4) = 2`


`h=-16t^2+64t+3 \\ h=-16(2)^2+64(2)+3 \\ \boxed{h=67}`