Question

The tables below show the values of f(x) and g(x) for different values of x.

f(x) = 2(3)x

xf(x)
-20.22
-10.67
02
16
218


g(x) = 3x + 9
xg(x)
-29.11
-19.33
010
112
218


Based on the tables, what is the solution to the equation 2(3)x = 3x + 9?
x = 0

x = 2

x = 12

x = 18

Answer 1

The solution of the given equation is x=2.

Explanation:

The first function is

`f(x)=2(3)^x`

The second function is

`g(x)=3^x+9`

The tables below show the values of f(x) and g(x) for different values of x.

We have to find the solution of

`2(3)^x=3^x+9`

If can be written as

`f(x)=g(x)`

It means solutions of the given equation is intersection point of both functions. So, the solution of the given function is a point where the value of f(x) and g(x) are same.

From the given that it is noticed that the point (2,18) is common in both tables.

Therefore the solution of the given equation is x=2.

And the another way to solve the problem is

`2(3)^x=3^x+9`

`2(3)^x-3^x=9`

`3^x=3^2`

Equate both sides.

`x=2`

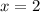
Therefore the solution of the given equation is x=2.

Answer 2

As you can see, in the table of the first function, f(2) = 18, and in the table of the second function g(2) = 18. Then, for x = 2, f(x) = g(x). and x =2 is the solution of the equation.

Answer: x = 2.