Answer:
Option C
Explanation:
Given : A coin dropped from a tall building is modeled by the equation
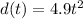 where, d is the distance traveled at time t seconds and t equals the time in seconds.
where, d is the distance traveled at time t seconds and t equals the time in seconds.
To find: The average rate of change of d(t) from t = 3 to t = 6
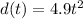
For t = 3 :
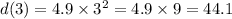
For t=6 :
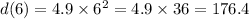
The difference of distance traveled between t=3 and t=6 seconds.
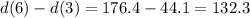
Now, we find the average speed :

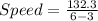
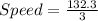
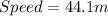
Therefore, Option C - The coin falls down with an average speed of 44.1 meter from 3 seconds to 6 seconds.