Question

Austin keeps a right conical basin for the birds in his garden as represented in the diagram. The basin is 40 centimeters deep, and the angle between the sloping sides is 77°. What is the shortest distance between the tip of the cone and its rim?

Answer 1

Answer: The shortest distance between the tip of the cone and its rim is 51.15 cm.

Explanation:

Since we have given that

Angle between the sloping side = 77°

Angle will get divided and the angle will be as

`(77^\circ)/(2)=38.5^\circ`

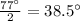
In first triangle , we will apply "Cosine formula ":

`\cos 38.5^\circ=(Base)/(Hypotenuse)\\\\\cos 38.5^\circ=(40)/(Hypotenuse)\\\\0.782=(40)/(Hypotenuse)\\\\Hypotenuse=(40)/(0.782)\\\\Hypotenuse=51.15\ cm`

Hence, the shortest distance between the tip of the cone and its rim is 51.15 cm.

Answer 2

If you draw a line along the center of the cone, you'd end up with two right triangles and the line also bisects the angle between the sloping sides. The shortest distance between the tip of the cone and its rim is the hypotenuse of a right triangle with one angle measuring 38.5°. So, using trigonometry and letting x as the measure of the shortest distance between the tip of the cone and its rim.
cos 38.5 = 40 / x
Solving for x
x = 51.11 cm