Question

Is the sum of an irrational number and rational number always irrational?

Answer 1

Yes.

It can be proved by contradiction.

Let:
a - a rational number
b - an irrational number
c - the sum of a and b


`a+b=c`

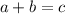
Let assume that c is a rational number. Then a and c can be expressed as fractions with integer numerator and denominator:

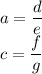
`a=(d)/(e)\\ c=(f)/(g)\\` where
`d,e,f,g \in \mathbb{Z}`


`(d)/(e)+b=(f)/(g)\\ b=(f)/(g)-(d)/(e)\\ b=(ef)/(eg)-(dg)/(eg)\\ b=(ef-dg)/(eg)`

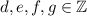
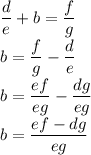
Since
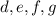
`d,e,f,g` are all integers, then the products
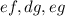
`ef,dg,eg` and the difference
`ef-dg` are integers as well. It means that the number
`b` is a rational number, but this on the other hand contradicts the earlier assumption that
`b` is an irrational number. Therefore
`c` must be an irrational number.