Question

If A(x1, y1), B(x2, y2), C(x3, y3), and D(x4, y4) form two line segments, AB and CD , which of these conditions needs to be met to prove that AB is perpendicular to CD?

see attachment for choices

Answer 1

`(y_4-y_3)/(x_4-x_3)* (y_2-y_1)/(x_2-x_1)=-1`

Explanation:

We know that,

If two line segments are perpendicular then the product of their slope is equal to -1,

Also, the slope of a line segment having the end points
`(x_n,y_n)` and
`(x_m,y_m)` is,

`m=(y_m-y_n)/(x_m-x_n)`

So, the slope of line segment AB having end points
`A(x_1,y_1)` and
`B(x_2,y_2)` is,

`m_1=(y_2-y_1)/(x_2-x_1)`

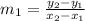
Similarly, the slope of line segment CD having end points
`C(x_3,y_3)` and
`(x_4,y_4)` is,

`m_2=(y_4-y_3)/(x_4-x_3)`

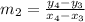
Hence, by the above property of perpendicular line segments ,

If AB and CD are perpendicular then,

`m_1* m_2=-1`

`\implies (y_4-y_3)/(x_4-x_3)* (y_2-y_1)/(x_2-x_1)=-1`

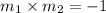
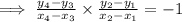
Third option is correct.

Answer 2

the answer is the third choice
it is c)
[y4-y3/x4-x3][y2-y1/x2-x1]= -1

proof
two lines are perpendicular if the product of their slope equals -1