Question

Solve tan(2θ)+tan(θ)=0 exactly

Answer 1

First, use the double angle formula for tangent:

`tan(2\theta) = \frac{2tan(\theta)}{1-{(tan(\theta))}^2}`
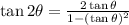
and then plug it in:


`\frac{2tan(\theta)}{1-{(tan(\theta))}^2} + tan(\theta) = 0`
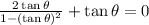
Multiply by
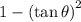
`1-{(tan(\theta))}^2` on both sides to get:


`2tan(\theta) + tan(\theta) - {(tan(\theta))}^3 = 0`

`3tan(\theta) - {(tan(\theta))}^3 = 0`

`3 - {(tan(\theta))}^2 = 0`

`{(tan(\theta))}^2 = 3`

`tan(\theta) = √(3)`

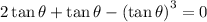
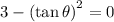
This means one solution is
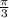
`(\pi)/(3)`. To get the other solutions just add integer multiples of
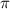
`\pi` (because the period of tangent is pi so answers will repeat every pi).