Question

What is the maximum number of turns in the graph of f(x)=2x^3-2x^2+7x-25 ?

Answer 1

The maximum number of turns in the graph of f(x) is:

2

Explanation:

Turning Point of a graph--

The turning point of a graph is a point where the graph changes it's behavior i.e. it changes from increasing to decreasing and from decreasing to increasing.

The polynomial of degree n has atmost " n-1 " turning points.

Here we are given a polynomial f(x) as:

`f(x)=2x^3-2x^2+7x-25`

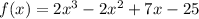
The polynomial is of degree 3.

Hence, the maximum number of turning points of the function f(x) is: 3-1=2

Answer 2

maximum number of turns in a cubic equation is always 2

the maximum number of turns will always be equal to one less degree of the poly
hope this helps