Question

If r1 and r2 are the roots of the quadratic equation ax+bx+c=0 show that r1+r2=-b/and r1r2=c/a

Answer 1

`x_(1,2) = \frac{-b+- \sqrt{ b^(2) -4ac} }{2a}`

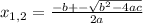
is the formula for calculating x1 and x2

To prove x1 + x2 = -b/a all we need to do is to express x1 and x2 from equation above

once we do we will get -2b/2a which is equal to -b/a because square root part will negate each other. one has + sign in front and other - sign

Showing that x1x2 = c/a goes similar way.
the numerator parts is actually difference of squares. after that we will have:
-b^2 -b^2 + 4ac = 4ac

in denominator we have 2a*2a = 4a^2
4ac/4aa = c/a