Question

\[f(x)=\sqrt{x ^4-16x ^{2}}\]

Let f be the function given by a) Find the domain of f. b) Find f '(x) c) Find the slope of the line normal to the graph of f at x = 5

Answer 1

`f ( x ) = \sqrt{ x^(4) -16 x^(2) }`
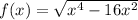
a ) The domain:
x^4 - 16 x² ≥ 0
x² ( x² - 16 ) ≥ 0
x² - 16 ≥ 0
x² ≥ 16
x ∈ ( - ∞, - 4 ] ∪ [ 4 , + ∞ )
b ) f ` ( x ) =
`\frac{1}{2 \sqrt{x ^(4)-16 x^(2) } } * ( x^(4)-16 x^(2) )` =`
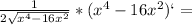
= ( 2 x³ - 16 x ) / √(x^4 - 16 x²)
c ) The slope of the tangent line at x = 5:
f ` ( 5 ) = ( 2 * 125 - 16 * 5 ) / √ ( 625 - 400 ) = 170 / 15 = 34 / 3
The slope of the line normal to the graph at x = 5:
m = - 3 / 34