Question

Find the ratio of the area of triangle XBY to the area of triangle ABC for the given measurements, if LINE XY is PARALLEL TO LINE AC

Answer 1

`(a)/(a_1)= (b)/(b_1)=(c)/(c_1)= (h_a)/(h_(a_1))=(10)/(6) = (5)/(3) \\ \\P_(ABC)= (a h_a)/(2) = ((5)/(3) a_(1)(5)/(3) h_(1))/(2) =(25)/(9) (a_(1) h_(a_1))/(2)=(25)/(9) P_(XBY) \\ \\ (P_(XBY))/(P_(ABC)) =(9)/(25)`

Answer 2

25:9

Explanation:

Given that ABC is a triangle and X,Y are points on AB and BC. XY is parallel to BC

Thus we have two similar triangles ABC and XBY.

The two triangles have corresponding sides as

10 and 6

i.e. side of ABC:side of XBZ = 10:6 =5:3

Hence area of ABC: area of XBZ=
`5^2:3^2 =25:9`

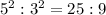
Answer:

The ratio of the area of triangle XBY to the area of triangle ABC for the given measurements, if LINE XY is PARALLEL TO LINE AC

=25:9