Question

How many combinations exist for the letters m, n, o, p, and q taken 3 at a time?

Answer 1

5 letters
3 slots
5 for 1st slot
4 for 2nd slot
3 for 3rd

5*4*3=60

60 ways

Answer 2

Answer: The required number of combinations is 10.

Step-by-step explanation: We are given to find the number of combinations that exists for the letters m, n, o, p, and q taken 3 at a time.

We know that

the formula for the combination of s objects taken r at a time is given by

`^sC_r=(s!)/(r!(s-r)!).`

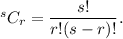
For the given combination, we have 5 letters and we are to take 3 at a time.

So, s = 5 and r = 3.

Therefore, the required number of combinations is

`^5C_3=(5!)/(3!(5-3)!)=(5!)/(3!2!)=(5*4*3!)/(3!*2*1)=10.`

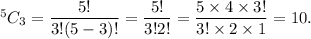
Thus, the required number of combinations is 10.