Question

Is my answer correct?

Write an exponential function to model this situation: a population of 420 animals decreases at an annual rate of 21%. Then predict the value of the function after 5 years (to the nearest whole number).

Answer 1

`y=420\cdot (0.79)^x`

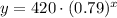
The value of the function after 5 years would be 129.

Explanation:

We have been that a population of 420 animals decreases at an annual rate of 21%. We are asked to write an exponential function for our given problem.

We know that an exponential function is in form
`y=a\cdot b^x`, where,

a = Initial value,

b = For decay b is in form
`1-r`, where, r represents decay rate in decimal form.

`r=21\%=(21)/(100)=0.21`

`y=a\cdot (1-r)^x`

`y=420\cdot (1-0.21)^x`

`y=420\cdot (0.79)^x`

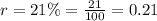
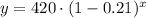
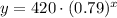
Therefore, our required function would be
`y=420\cdot (0.79)^x`.

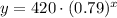To find the value of the function after 5 years, we will substitute
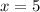`x=5` in our function.

`y=420\cdot (0.79)^5`

`y=420\cdot 0.3077056399`

`y=129.236368758`

`y\approx 129`

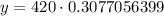
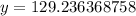
Therefore, the value of the function after 5 years would be 129.

Answer 2

Here is the answer to the given problem above.
Here is the exponential function to model this situation:
f(x) = 420(0.79)x
Now, solve with the given values.
P(t)=420×(.79)^t P(5)=420×(.79)^5=129
So the answer would be 129 animals.
Hope this answer helps. Thanks for posting your question!