Question

Math Help!!! How many x-intercepts does the graph of the function have?

List them out. How many complex zeros are there to the function?
List them out. Please explain both questions.

Answer 1

If you are given a parabolic function you can algebraically determine the type of zeros of the function with the discriminant, which is
`b^2-4ac`.

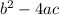
The discriminant is derived from the quadratic formula,
`x= (-b+/- √(b^2-4ac) )/(2a)`.
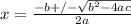
The discriminant is what's inside the square root (the radicand).

If the radicand is negative, there will be 2 imaginary numbers (there are two because of the plus or minus before the square root)
If the radicand is positive, there will be 2 real numbers.
If the radicand is zero, the answer will be 0.

Therefore,
If discriminant is negative, there are 2 complex zeros.
If discriminant is positive, there are 2 real zeros.
If discriminant is zero, there is one real zero.

A zero is basically the x-intercept.

Answer 2

It can have however many x intercepts it wants,

BUT, to be a function it must pass the vertical line test.
this means you have to look at the graph and see if a vertical line drawn anywhere hits the graph more than once.
if it hits it more than once, it is NOT a function.

An example is a polynomial function to the infinite degree. That is
f(x) = lim (n --> infinity) [ x^n]
but only 1 y intercept (vertical line test remember)