Question

HELP!! Need a full explanation. The coordinates of the vertices of quadrilateral ABCD are A(0, 4), B(4, 2), C(2,-1), D(-2, 1). Jorge states that quadrilateral ABCD is a parallelogram. Prove or disprove Jorge’s statement.

Answer 1

ABCD is a parallelogram.

Explanation:

As per property of parallelogram,

AD = BC and AB = DC

Slope of AD should be equal to BC and slope of AB should be equal to slope of DC.

Length of AD =
`\sqrt{(x-x')^(2)+(y-y')^(2)}`

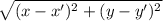
AD =
`\sqrt{(0+2)^(2)+(4-1)^(2)}`

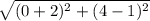
AD =
`√(13)`

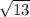
Length of BC =
`\sqrt{(4-2)^(2)+(2+1)^(2)}`

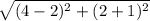
BC =
`√(4+9)`

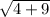
BC =
`√(13)`

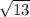
Slope of AD =
`(y-y')/(x-x')`

=
`(4-1)/(0+2)`

=
`(3)/(2)`

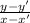
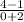
Slope of BC =
`((2+1))/((4-2))`

=
`(3)/(2)`

Length of AD and BC are equal and slope of AD and BC are same.

Similarly, length of AB and DC and slope of AB and DC should be equal.

Length of AB =
`\sqrt{(0-4)^(2)+(4-2)^(2)}`

=
`√(20)`

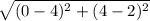
Length of DC =
`\sqrt{(-2-2)^(2)+(1+1)^(2)}`

=
`√(20)`

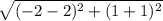
Now slope of AB =
`(4-2)/(0-4)`

=
`-(1)/(2)`

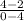
Slope of DC =
`(1+1)/(-2-2)`

=
`-(1)/(2)`

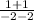
Hence, length of AB and DC are same and slopes of AB and DC are same in measure.

Therefore, the given coordinates are of a parallelogram.