Answer:
96
Explanation:
Given that the population of a type of local bass can be found using an infinite geometric series.
I term a1 = 72
Common ratio r =
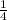
We know that sum of n terms of geometric series where |r|<1 is

Sum of infinite terms would be limit of this Sn as n tends to infinity.
When r <1 we have r^n will tend to 0 as n tends to infinity.
Hence Sum of infinite terms
=

Sum of infinite series = 96