Question

What is the solution set of the quadratic inequality 3x^2-8x+4>0

Answer 1

So first of all we want to solve the quadratic equation, when it is zero, so for now, let us calculate (as you maybe have done) by equating to zero.

The solutions are


`x = (2)/(3), x = 2`

now we want to know which of these two values actually are below or over zero. By having two values reaching zero and we now that it is a concave up, meaning that it is "a smiling curve", we see what sign it is between our two roots.

Take for example
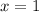
`x = 1` (this value is between
`x = 2/3` and
`x= 2`. By inserting into
`3x^2-8x+4`, we get that it is
`-1`. This concludes, that values which are in the range
`(2)/(3)<x<2` are negative, and the other, which are
`x<2/3` and
`2<x` are positive, which is what we want.

Answer:


`x \ \textless \ (2)/(3),2\ \textless \ x`