Question

A painting is purchased for $250. if the value of the painting doubles every 5 years, then its value is given by the function v(t) = 250 • 2t/5, where t is the number of years since it was purchased and v(t) is its value (in dollars) at that time. what is the value of the painting ten years after its purchase? $1,000 $1,400 $1,800 $2,000

Answer 1

After 5 years, value doubles.
Hence after 5 years, value is 250 x 2 = 500
After another 5 years, value doubles.
500 x 2 = 1000
Ans: $1000

Method 2, using function given.
v(10) = 250 x 2(10/5) = $1000

Answer 2

Option A is correct.

the value of the painting ten years after its purchase is, $1,000

Explanation:

Given the function:

`v(t) = 250 \cdot 2((t)/(5))` .....[1]

where,

t is the number of years since it was purchased and

v(t) is its value(in dollars) at that time.

We have to find the value of the painting ten years after its purchase.

⇒ t = 10 years

Substitute in [1] we have;

`v(10) = 250 \cdot 2((10)/(5))`

⇒
`v(10) = 250 \cdot 2(2)`

⇒
`v(10) = 250 \cdot 4`

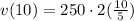
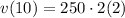
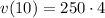
Simplify:

`v(10) =\$ 1,000`

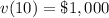
Therefore, the value of the painting ten years after its purchase is, $1,000