ANSWER: The correct answer is
 .
.
Step-by-step explanation
The composition of a function of
 and its inverse will produce the independent variable
and its inverse will produce the independent variable
 .
.
For instance, let
 .
.
The inverse of this function is
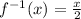 .
.
If we compose these two functions, we will obtain;
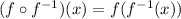
This means we have to substitute the whole inverse function in to the function itself.
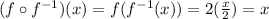
The other way round will also produce the same result.
Thus;
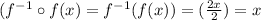
This does not only apply to the given example it applies to all functions and their inverse.