Question

1. Write a paragraph proof for the following conjecture. Given: bisects . . Prove: is a right triangle. Answer: Angle PQR equals 90 degrees Given:

Answer 1

if pqs is 45 degrees then sqr is 45 degrees by the definition of a bisector. pqs is equal to sqr becuase of definition of congruent angles therefore pqs + sqr= 90 by the addition property. what this means is that pqr is a right angle because of the definition of a right angle

Answer 2

Answer with Step-by-step explanation:

We are given that in triangle PQR

QS bisect the angle PQR

`\angle PQS=45^(\circ)`

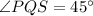
We have to prove that
`\angle PQR=90^(\circ)`

`\angle PQS=\angle PQR`

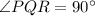
Because QS bisect the angle PQR.

Therefore,
`\angle PQR=45^(\circ)`

`\angle PQR=\angle PQR+\angle PQS`

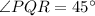
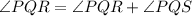
Substitute the values then we get

`\angle PQR=45+45`

`\angle PQR=90^(\circ)`

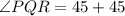
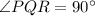
Hence, triangle PQR is right triangle because one angle of triangle is of 90 degrees.

Hence, proved.