Question

Uranium-238 has a half-life of 4.5 billion years. Given that scientists estimate Earth's age to be 4.6 billion years, what is the most likely percentage of parent to daughter isotopes of this element currently existing on Earth? A. 10 percent B. 25 percent C. 50 percent D. 75 percent

Answer 1

The correct answer is option C.

Step-by-step explanation:

Half life of the uranium-238=
`t_{(1)/(2)}=4.5 \text{billion years}`

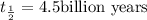
Decay constant =
`\lambda`

`\lambda =\frac{0.693}{t_{(1)/(2)}}`

`\lambda =\frac{0.693}{4.5 \text{billion years}}=0.154 ({\text{billion year})^(-1)`

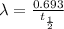
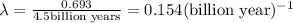
Let the initial amount of U-238 be x

And the present amount of U-238 be x'.

`A=A_o* e^(-\lambda t)`

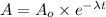
`A_o` = Initial amount

A = Amount left after time t

`x'=x* e^{-0.154 ({\text{billion year})^(-1)* 4.5\text{billion years}}`

`x'=x* 0.500`

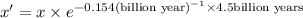
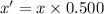
Percentage of left amount:

`\%=(A)/(A_o)* 100`

`\%=(x* 0.5000)/(x)* 100=50.00\%`

Hence,the correct answer is option C.