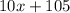Answer:
Option C is correct
the function f[g(x)] represents correctly is:
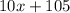
Explanation:
Given the function:
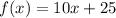 and
and
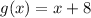
then;
![f[g(x)]](https://img.qammunity.org/2017/formulas/mathematics/high-school/89kvxll3glf3g15dnlq0ffq31uto8x9dml.png)
Substitute the function g(x) we have;
⇒
![f[x+8]](https://img.qammunity.org/2017/formulas/mathematics/high-school/w85itbmxuz9k5f3b1gvokslwr6zb0vv92q.png)
Replace x with x+8 in f(x) we have;
⇒
![f[x+8] = 10(x+8)+25](https://img.qammunity.org/2017/formulas/mathematics/high-school/bpvn4qc1cn7kyby65hkql8lkt166go0m5o.png)
Using distributive property:
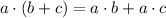
⇒
![f[g(x)] = 10x+80+25 = 10x+105](https://img.qammunity.org/2017/formulas/mathematics/high-school/bzc397hvc8jnfzh2mtzr6k8201uwvp14zu.png)
Therefore, the function f[g(x)] represents correctly is: