Question

1. Find the polynomial f(x) that has the roots of -3, 5 of multiplicity 2. Explain how you would verify the zeros of f(x).

Answer 1

At first you need to turn roots into factors, and then multiply them
`x = -2 ==\ \textgreater \ x + 2 x = 5 ==\ \textgreater \ x - 5`
`multiplicity 2 ==\ \textgreater \ (x - 5)^2`
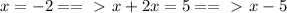
Then you have

f(x) = a(x + 2)(x - 5)^2
f(x) = a(x + 2)(x^2 - 10x + 25)
f(x) = a(x^3 - 8x^2 + 5x + 50)
You can use either synthetical or the factor theorem
f(-2) = a(-8 - 8(4) + 5(-2) + 50) = a(0) = 0... check, f = -2
f(5) = a(125 - 8(25) + 5(5) + 50) = a(0) = 0 check, f = 5 works
Then divide it to the the second multi
And you should get x^2 - 3x - 10 = (x - 5)(x + 2), where the other two zeros are x = 5 , and x = -2