Question

Point G is located at (3, -1) and point H is located at (-2, 3). Find the point that is 2/3 the distance from point G to point H. Select one. a. (0.33, -1.67) b. (-0.33, 1.67) c. (-0.5, -1) d. (6.33, -2.67)

Answer 1

Coordinates of point C that is two-third the distance from point G to point H is (-0.33,1.67)

Explanation:

Given that Point G is located at (3, -1) and point H is located at (-2, 3). we have to find out the point that is two-third the distance from point G to point H which means in ratio 2:1

When any point divides a segment in ratio m:n, we use the section formula to find the coordinates of that point.

The coordinates of the point C that divides the line segment joining the points G(3,-1) and point H(-2,3) in ration m:n i.e 2:1 is

`C=((mx_2+nx_1)/(m+n), (my_2+ny_1)/(m+n))`

`=((2(-2)+1(3))/(2+1), (2(3)+1(-1))/(2+1))`

`=((-1)/(3),(5)/(3))`

`=(-0.33,1.67)`

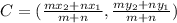
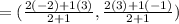
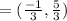
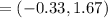
Hence, coordinates of point C that is two-third the distance from point G to point H is (-0.33,1.67)

Answer 2

The point is dividing the segment G H in ratio: m : n = 2 : 1
( x, y ) = ( (1*3 + 2*(-2))/(2+1) ; (1 * (-1) + 2 * 3) /(2 + 1) ) =
= ( (3-4)/3 ; (-1+6)/3 ) = ( - 0.33; 1.67 )
Answer: B ) ( - 0.33; 1.67 )