Question

A kite has vertices at (2, 4), (5, 4), (5, 1), and (0, –1).

What is the approximate perimeter of the kite? Round to the nearest tenth.

Answer 1

The answer is 16.8 units

Answer 2

16.7 units

Explanation:

We are given that A kite has vertices at (2, 4), (5, 4), (5, 1), and (0, –1).

So, Let A = (2,4)

B =(5,4)

C =(5,1)

D =(0,-1)

So, Find the sides AB ,BC,CD,AC

To find AB use distance formula :

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`(x_1,y_1)=(2,4)`

`(x_2,y_2)=(5,4)`

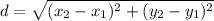
Substitute the values in the formula :

`AB=√((5-2)^2+(4-4)^2)`

`AB=√((3)^2+(0)^2)`

`AB=√(9)`

`AB=3`

To find BC use distance formula :

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`(x_1,y_1)=(5,4)`

`(x_2,y_2)=(5,1)`

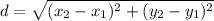
Substitute the values in the formula :

`BC=√((5-5)^2+(1-4)^2)`

`BC=√((0)^2+(-3)^2)`

`BC=√(9)`

`BC=3`

To find CD use distance formula :

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`(x_1,y_1)=(5,1)`

`(x_2,y_2)=(0,-1)`

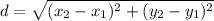
Substitute the values in the formula :

`CD=√((0-5)^2+(-1-1)^2)`

`CD=√((-5)^2+(-2)^2)`

`CD=√(25+4)`

`CD=√(29)`

To find AD use distance formula :

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

`(x_1,y_1)=(2,4)`

`(x_2,y_2)=(0,-1)`

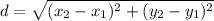
Substitute the values in the formula :

`CD=√((0-2)^2+(-1-4)^2)`

`CD=√((-2)^2+(-5)^2)`

`CD=√(4+25)`

`CD=√(29)`

Now perimeter of Kite = Sum of all sides

=AB+BC+CD+AD

=
`3+3+√(29)+√(29)`

=
`16.7`

Thus the perimeter of the kite is 16.7 units.