If f(x) =tan(2x) then f'(pi/6)?

Question

asked Nov 10, 2017 112k views

2 Answers

Milka · Answer 1 · 2017-11-11T13:39:50+0000

The derivative of f(x) = tan(2x) is
2sec^2(2x) . When
$x = \pi /6,$ the derivative is 8/3.

To find the derivative of f(x) = tan(2x), we can use the chain rule.

The derivative of tan(x) is
sec^2(x) , so the derivative of tan(2x) is
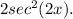
2sec^2(2x).

Substituting π/6 for x, we have -

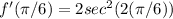
$f'(\pi /6) = 2sec^2(2(\pi /6))$

= 2sec^2(π/3).

Using the identity
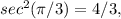
$sec^2(\pi /3) = 4/3,$

we find that
$f'(\pi /6)$ = 2(4/3)

= 8/3.