Question

What is the number of real solutions? –11x^2 = x + 11

Answer 1

Given the equation:
`-11x^2 = x+11`

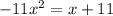
or we can write above equation as:

`-11x^2-x-11=0` or

`11x^2+x+11 =0`

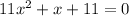
The general equation of quadratic formula for
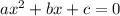`ax^2+bx+c=0`; where a, b and c are constant;

Use Discriminant formula:
`D =b^2-4ac`

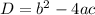
If
`D> 0`, then there are 2 roots.

If D = 0, then there is only 1 root.

If D <0, then there are no real roots.

Now, from the given equation
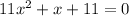`11x^2+x+11 =0` we have

a =11, b= 1 and c =11

Then, using discriminant formula we have;

`D =b^2-4ac =(1)^2 -4(11)(11) = 1-4\cdot 121 = 1-484= -483`

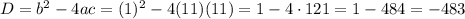
⇒D<0 [ No real roots]

Therefore, for the given equation
`-11x^2 = x+11` , there are no real solutions.

Answer 2

-11 x² = x + 11
11 x² + x + 11 = 0
We will find the value of the discriminant:
D = b² - 4 a c = 1² - 4 * 11 * 11 * 1 - 484 = - 483
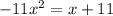D < 0. There are no real solutions.