Question

Cory has 15 die-cast cars in his collection. Each year his collection increases by 20%. Roger has 40 cars in his collection. Each year he collects 1 additional car.

Part A: Write functions to represent Cory and Roger's collections throughout the years.
Part B: How many cars does Cory have after 6 years? How many does Roger have after the same number of years?
Part C: After approximately how many years is the number of cars that Cory and Roger have the same? Justify your answer mathematically.

Answer 1

Explanation:

Part A:

For Roger:

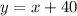
For Cory:

where y is the total number of cars each boy collects over the year, x as the number of years passed.

Part B:

For Roger: 46

For Cory: 44.79~ 45 cars

Answer 2

Part A:
For Roger:
`y=x+40`
For Cory:
`y=15 (1.2)^(x)`
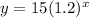
where y is the total number of cars each boy collects over the year, x as the number of years passed.

Part B:
For Roger: 46
For Cory: 44.79~ 45 cars

Part C:
Here, we are trying to find the number of years (x) where Cory and Roger have the same number of cars.
By equating Roger and Cory's functions, we can solve for x

`x+40=15 (1.2)^(x)`.
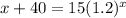
Since we cannot solve the value of x directly, we use trial and error to estimate the year.
When x=1

`41 \\eq 18 \\`
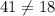
When x=2

`42 \\eq 21.6`
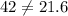
When x=3

`43 \\eq 25.92`
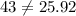
When x=4

`44 \\eq 31.10`
When x=5
45=/=37.3
When x=6
46=/=44.8
When x=7
47=/=53.7

The years that pass by before Cory and Roger have nearly the same number of cars is 6.