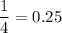Question

a bag of coins contains 2 quarters, 5 dimes, 3 nickels, and 4 pennies. if 2 coins are randomly chosen from the bag, one after the other, and not replaced, and if the total value of the chosen coins is 26 cents, what is the probability that a third coin randomly chosen from the bag will be a penny?

Answer 1

The probability that a third coin randomly chosen is a penny is:

`(1)/(4)=0.25`

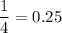
Explanation:

a bag of coins contains 2 quarters, 5 dimes, 3 nickels, and 4 pennies.

This means that there are total 14 coins.

( Since 2 quarters+ 5 dimes + 3 nickels +4 pennies=14 coins)

Now, two coins were chosen one after the other without replacement.

So, the total number of coins left=14-2=12 coins.

As we know that:

1 nickel= 5 cents.

1 dime= 10 cents.

1 quarter= 25 cents

1 penny= 1 cent.

Hence, the two coins that were drawn to add up to 26 cents have to be a quarter and a penny. ( Since, 25 cents +1 cents=26 cents)

Hence, after the two draw we are left with 3 pennies.

Hence, the probability that a third coin randomly chosen will be a penny is calculated as:

`=(3)/(12)`

( Since we have 3 choices i.e. 3 pennies out of total 12 coins left)

Hence, the probability is:

`(1)/(4)=0.25`

Answer 2

Total number of coins = 14
Coins chosen in the first two draws = quarter and penny

Probability that the third coin will be a penny = number of remaining penny/ total remaining coins = 3/12 = 1/4