Let
x--------> pounds of peanuts
y--------> pounds of almonds
z--------> pounds of raisins
we know that
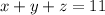 -----> equation
-----> equation

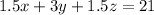 -----> equation
-----> equation
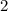
 -----> equation
-----> equation

Substitute the equation
 in equation
in equation
 and equation
and equation
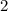
So
![[2y]+y+z=11](https://img.qammunity.org/2017/formulas/mathematics/high-school/928gm7akwlnbl345upviev9ssm8qa1opqa.png)
 -------> equation
-------> equation

![1.5[2y]+3y+1.5z=21](https://img.qammunity.org/2017/formulas/mathematics/high-school/yf7jr42fxv18dk57y53fx4akmtngw51jdm.png)
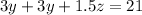
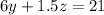 -----> equation
-----> equation

Solve the system
 -----> equation
-----> equation

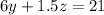 -----> equation
-----> equation

Multiply by -2 equation

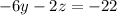
Adds equation
 and equation
and equation

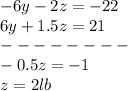
find the value of y
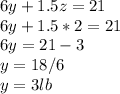
find the value of x
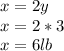
therefore
the answer is the option
C. 6 lbs peanuts, 3 lbs almonds, 2 lbs raisins