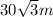Question

An equilateral triangle has an altitude of 15 m. What is the perimeter of the triangle?

Answer 1

we know that

In the equilateral triangle every sides and angles are equal

so

the measure of internal angles is equal to
`60` degrees

see the attached picture to better understand the problem

In the right triangle ABC

`sin 60=BC/AB`

where

BC is the altitude (opposite side angle
`60` degrees

AB is the hypotenuse

Clear AB

`AB=BC/sin 60\\ AB=15/((√(3))/(2) )\\ AB=30/√(3)m`

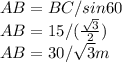
Perimeter of the triangle is equal to

`P=AB+BD+AD`

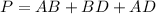
but remember that

`AB=BD=AD`

so

`P=3*AB\\ P=3*(30)/(√(3)) \\ \\ P=(90)/(√(3)) \\ \\ P=30√(3) m`

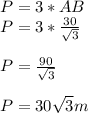
therefore

the answer is

`30√(3) m`

Answer 2

equilateral triangle mean every sides and angles are equal
so the measure of angles is 60 degrees
given that has an altitude of 15 m so this mean that

sin 60 = altitude / hypotenuse

sqrt3 /2 = 15/hyp.

hyp. = 15/(sqrt3 /2)

hyp. = 30/sqrt3 = 30sqrt3 / 3 = 10sqrt3

so in this way ve got that a side length is equal 10sqrt3 and the perimeter

P = 3*10sqrt3

P = 30sqrt3 m so the 3rd choice is right,correct sure

hope helped