Question

Write the expression as either the sine, cosine, or tangent of a single angle. sin(pi/2)cos(pi/7)+cos(pi/2)sin(pi/7)

Answer 1

`\text{sin}((9\pi)/(14))`.

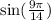Explanation:

We have been given a trigonometric expression
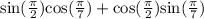`\text{sin}((\pi)/(2))\text{cos}((\pi)/(7))+\text{cos}((\pi)/(2))\text{sin}((\pi)/(7))`. We are asked to write our given expression as either the sine, cosine, or tangent of a single angle.

Using identity
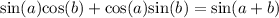`\text{sin}(a)\text{cos}(b)+\text{cos}(a)\text{sin}(b)=\text{sin}(a+b)`, we can rewrite our given expression.

Let
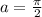`a=(\pi)/(2)` and
`b=(\pi)/(7)`.

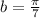Upon substituting these values in above identity, we will get:

`\text{sin}((\pi)/(2))\text{cos}((\pi)/(7))+\text{cos}((\pi)/(2))\text{sin}((\pi)/(7))=\text{sin}((\pi)/(2)+(\pi)/(7))`

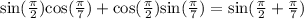
Upon simplifying right side of our equation, we will get:

`\text{sin}((\pi)/(2)+(\pi)/(7))=\text{sin}((\pi*7)/(2*7)+(\pi*2)/(7*2))`

`\text{sin}((\pi)/(2)+(\pi)/(7))=\text{sin}((7\pi)/(14)+(2\pi)/(14))`

`\text{sin}((\pi)/(2)+(\pi)/(7))=\text{sin}((7\pi+2\pi)/(14))`

`\text{sin}((\pi)/(2)+(\pi)/(7))=\text{sin}((9\pi)/(14))`

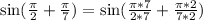
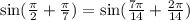
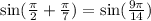
Therefore, our required expression would be
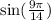`\text{sin}((9\pi)/(14))`.

Answer 2

I will use the sin (a + b) identity:
sin (a + b) = sina cosb + cosa sinb and
here a = π/2 and b = π/7

so sin (π/2 + π/7)
= sin (9π / 14)