We will use the formula for distance;
XY =

Applying the same formula
YZ =

XZ =
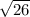
XZ^2 + YZ^2 is not equal with XY^2 which means the triangle is not right.
In order to make the triangle right, we have to take X and Z on the same x-line which means Z will be (6, 1) and Z and Y to be on the same y-line which means Y will be (6, 6). The point will be:
X(1, 1)
Y(6, 6)
Z(6, 1)
XY =
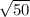
YZ =

XZ =

It means that: YZ^2+XZ^2=XY^2 and the triangle is right.